Передаточное отношение передачи. это необходимо знать для максимального использования ресурса авто

Литература

• ГОСТ 16530-83. ПЕРЕДАЧИ ЗУБЧАТЫЕ; общие термины, определения и обозначения. — официальное. — Москва: ИПК Издательство стандартов, 1983. — 51 с.
• ГОСТ 9563-60. КОЛЁСА ЗУБЧАТЫЕ; модули. — официальное. — Москва: ИПК Издательство стандартов, 1960. — 4 с.
• Зубчатые колеса // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
• Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр «Академия», 2004. — С. 416. — ISBN 5-7695-1384-5.
• Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 438—480. — 864 с. — ISBN 5-217-00403-7.
• Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — Т. 2. — 912 с. — ISBN 5-217-02964-1 (5-217-02962-5), ББК 34.42я2, УДК 621.001.66 (035).
• Фролов К. В., Попов С. А., Мусатов А. К., Тимофеев Г. А., Никоноров В. А. Теория механизмов и механика машин / Колесников К. С. — Издание четвёртое, исправленное и дополненное. — М.: Издательство МГТУ им. Н. Э. Баумана, 2002. — Т. 5. — С. 452—453, 456-459, 463-466, 497-498. — 664 с. — (Механика в техническом университете). — 3000 экз. — ISBN 5-7038-1766-8.
•  (недоступная ссылка)

Ошибки при проектировании зубчатых колёс

Зуб, подрезанный у основания

Подрезание зуба

Согласно свойствам эвольвентного зацепления, прямолинейная часть исходного производящего контура зубчатой рейки и эвольвентная часть профиля зуба нарезаемого колеса касаются только на линии станочного зацепления. За пределами этой линии исходный производящий контур пересекает эвольвентный профиль зуба колеса, что приводит к подрезанию зуба у основания, а впадина между зубьями нарезаемого колеса получается более широкой. Подрезание уменьшает эвольвентную часть профиля зуба (что приводит к сокращению продолжительности зацепления каждой пары зубьев проектируемой передачи) и ослабляет зуб в его опасном сечении. Поэтому подрезание недопустимо. Чтобы подрезания не происходило, на конструкцию колеса накладываются геометрические ограничения, из которых определяется минимальное число зубьев, при котором они не будут подрезаны. Для стандартного инструмента это число равняется 17. Также подрезания можно избежать, применив способ изготовления зубчатых колёс, отличный от способа обкатки. Однако и в этом случае условия минимального числа зубьев нужно обязательно соблюдать, иначе впадины между зубьями меньшего колеса получатся столь тесными, что зубьям большего колеса изготовленной передачи будет недостаточно места для их движения и передача заклинится.

Подрезание зуба

Заострение зуба

Для уменьшения габаритных размеров зубчатых передач колёса следует проектировать с малым числом зубьев. Поэтому при числе зубьев меньше 17, чтобы не происходило подрезания, колёса должны быть изготовлены со смещением инструмента — увеличением расстояния между инструментом и заготовкой (корригированные зубчатые колеса).

Заострение зуба

Компьютерная модель зубчатой передачи (см. нанотехнологии)

При увеличении смещения инструмента толщина зуба будет уменьшаться. Это приводит к заострению зубьев. Опасность заострения особенно велика у колёс с малым числом зубьев (менее 17). Для предотвращения скалывания вершины заострённого зуба смещение инструмента ограничивают сверху.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

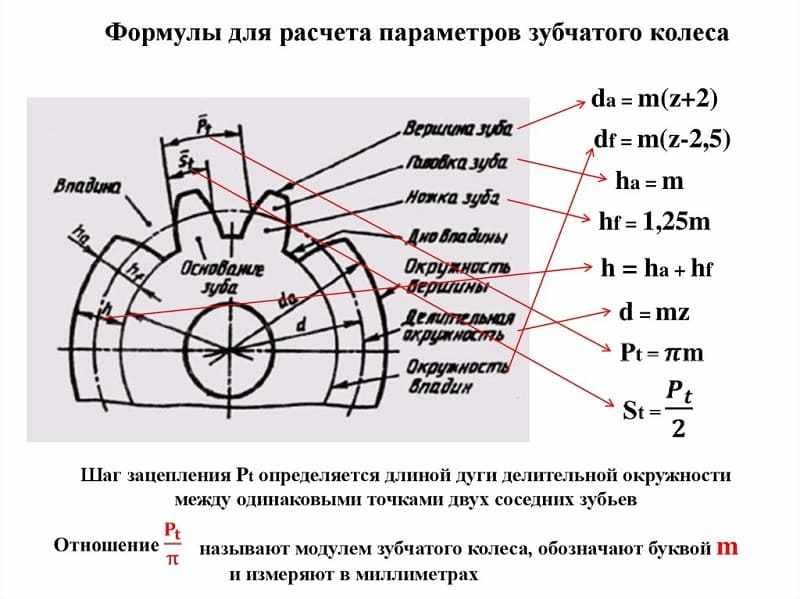
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t× z,

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

Диаметр окружности впадин D i соответствует D e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Выполнив подстановку в правой части равенства, имеем:

D i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D i = m(z-2,5m).

Полная высота:

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s в, получаем формулы для ширины впадины

• для отлитых зубцов: s в =πm-1,53m=1,61m:
• для выполненных путем фрезерования- s в = πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Волновая передача

Ее работа основывается на принципе трансформации параметров движения благодаря волновому деформированию гибкого элемента механизма. По сути, такая передача является разновидностью планетарной передачи.

В состав волновой передачи входит жесткое колесо зубчатое, имеющее внутренние зубья, и вращающееся гибкое колесо с наружными зубьями. Оба колеса между собой входят в зацепление благодаря генератору волн, соединенному непосредственно с корпусом передачи.

За счет имеющихся конструктивных особенностей волновая передача наделена следующими достоинствами:

• Небольшие габариты и масса.
• Высокая кинематическая точность.
• Передаточное отношение передачи в одной ступени имеет большой показатель и вполне может достигать 300.
• Идеальная демпфирующая способность.
• Формирование в одной ступени большого передаточного отношения.

К недостаткам же относятся:

• Весьма сложная конструкция.
• Высокие потери мощности на трение и деформацию гибкого колеса (КПД составляет порядка 0,7-0,85).

Расчет оборотов двигателя по передаточному числу

Как рассчитать передаточное отношение шестерен механической передачи.

В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев

Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев

Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.

Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.

Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.

Итак, рассмотрим пример расчета с использованием двух шестерен.

Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.

В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.

Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.

Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.

Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.

Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.

Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.

В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.

Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.

Определим теперь частоту вращения.

Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.

Будем использовать формулу: S1 × T1 = S2 × T2,

S1 – частота вращения желтой (ведущей) шестерни,

Т1 – количество зубьев желтой (ведущей) шестерни;

S2- частота вращения красной шестерни,

Т2 – количество зубьев красной шестерни.

В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.

340 rpm × 7 = S2 × 40

Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.

Источник

Реечная передача (кремальера)

Реечная передача (кремальера)  — один из видов механических передач, преобразующий вращательное движение ведущей шестерни в поступательное движение рейки. Используется в рулевом управлении большинства переднеприводных легковых автомобилей. Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.

Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс. Также реечная передача применяется в зубчатой железной дороге.

Цепная передача

Хорошо известна цепная передача. Она относится к гибким конструкциям. Передаточное отношение цепной передачи рассчитывается расчёту зубчатых систем. Ведущая и ведомая звёздочка рассматриваются как зубчатые колеса. Значение этого параметра достигает 15.

Особенностью такой конструкции считается требование иметь определённое провисание цепи.  Настройка этого параметра проводится с помощью специального регулирующего винта.

Достоинства подобного соединения сводятся к следующему:

• низкая критичность к возможным ошибкам при установке валов.
• передача мощности производится с использованием нескольких звездочек;
• длина передачи вращения может быть достаточно большой.

К недостаткам можно отнести быстрый износ соединительных элементов цепи. Это требует периодической смазки. Вторым недостатком считается высокий уровень шума.

Кроме передаточного числа для них рассчитывается величина статистической разрушающей силы. Этот параметр зависит от требуемого коэффициента безопасности. Его задают в интервале от 6 до 10. Он обеспечивает качественную работу всего механизма, высокую надёжность соединения и долговечность.

Тип редуктора

Наличие кинематической схемы привода упростит выбор типа редуктора. Конструктивно редукторы подразделяются на следующие виды:

Червячный одноступенчатый со скрещенным расположением входного/выходного вала (угол 90 градусов).

Червячный двухступенчатый с перпендикулярным или параллельным расположением осей входного/выходного вала. Соответственно, оси могут располагаться в разных горизонтальных и вертикальных плоскостях.

Цилиндрический горизонтальный с параллельным расположением входного/выходного валов. Оси находятся в одной горизонтальной плоскости.

Цилиндрический соосный под любым углом. Оси валов располагаются в одной плоскости.

В коническо-цилиндрическом редукторе оси входного/выходного валов пересекаются под углом 90 градусов.

ВАЖНО! Расположение выходного вала в пространстве имеет определяющее значение для ряда промышленных применений

• Конструкция червячных редукторов позволяет использовать их при любом положении выходного вала.
• Применение цилиндрических и конических моделей чаще возможно в горизонтальной плоскости. При одинаковых с червячными редукторами массо-габаритных характеристиках эксплуатация цилиндрических агрегатов экономически целесообразней за счет увеличения передаваемой нагрузки в 1,5-2 раза и высокого КПД.

Таблица 1. Классификация редукторов по числу ступеней и типу передачи

Тип редуктора	Число ступеней	Тип передачи	Расположение осей
Цилиндрический	1	Одна или несколько цилиндрических	Параллельное
2	Параллельное/соосное
3
4	Параллельное
Конический	1	Коническая	Пересекающееся
Коническо-цилиндрический	2	Коническая Цилиндрическая (одна или несколько)	Пересекающееся/скрещивающееся
3
4
Червячный	1	Червячная (одна или две)	Скрещивающееся
1	Параллельное
Цилиндрическо-червячный или червячно-цилиндрический	2	Цилиндрическая (одна или две) Червячная (одна)	Скрещивающееся
3
Планетарный	1	Два центральных зубчатых колеса и сателлиты (для каждой ступени)	Соосное
2
3
Цилиндрическо-планетарный	2	Цилиндрическая (одна или несколько) Планетарная (одна или несколько)	Параллельное/соосное
3
4
Коническо-планетарный	2	Коническая (одна) Планетарная (одна или несколько)	Пересекающееся
3
4
Червячно-планетарный	2	Червячная (одна) Планетарная (одна или несколько)	Скрещивающееся
3
4
Волновой	1	Волновая (одна)	Соосное

Крутящий момент редуктора

Крутящий момент на выходном валу – вращающий момент на выходном валу. Учитывается номинальная мощность , коэффициент безопасности , расчетная продолжительность эксплуатации (10 тысяч часов), КПД редуктора.

Номинальный крутящий момент – максимальный крутящий момент, обеспечивающий безопасную передачу. Его значение рассчитывается с учетом коэффициента безопасности – 1 и продолжительность эксплуатации – 10 тысяч часов.

Максимальный вращающий момент – предельный крутящий момент, выдерживаемый редуктором при постоянной или изменяющейся нагрузках, эксплуатации с частыми пусками/остановками. Данное значение можно трактовать как моментальную пиковую нагрузку в режиме работы оборудования.

Необходимый крутящий момент – крутящий момент, удовлетворяющим критериям заказчика. Его значение меньшее или равное номинальному крутящему моменту.

Расчетный крутящий момент – значение, необходимое для выбора редуктора. Расчетное значение вычисляется по следующей формуле:

Mc2 = Mr2 x Sf ≤ Mn2

где Mr2 – необходимый крутящий момент; Sf – сервис-фактор (эксплуатационный коэффициент); Mn2 – номинальный крутящий момент.

Храповый механизм

Во многих машинах и агрегатах применяется не только непрерывное вращательное движение, но и прерывистое тоже, которое осуществляется с помощью храповика, собачки и рычага.

Храповый механизм помимо вращения еще и осуществляет предохранительную функцию. Так, например, в грузоподъемных лебедках, храповик совместно с собачкой не позволяют барабану проворачиваться в обратную сторону, надёжно фиксируя его в требуемом пространственном положении.

Рассмотренные виды механических передач применяются практически в любой отрасли народного хозяйства и получили широчайшее распространение благодаря своим техническим возможностям.

Обзор передач

На сегодняшний день существуют такие виды механических передач:

• Зубчатые.
• Ременные.
• Фрикционные.
• Червячные.
• Цепные.
• Храповые.
• Волновые.

В целом же, механические передачи разделяются по таким критериям:

• В зависимости от передачи движения от ведущего звена к ведомому: передачи трением и передачи зацеплением.
• В зависимости от соотношения скоростей ведомого и ведущего звеньев: замедляющие передачи (они же редукторы), ускоряющие передачи (мультипликаторы).
• В зависимости от расположения осей валов: передачи с перекрещивающимися, пересекающимися и параллельными осями.

Стоит указать, что замедляющие передачи на практике применяются гораздо чаще, нежели ускоряющие. Этот факт объясняется тем, что скорости вращения двигателей зачастую гораздо выше требуемой скорости вала исполнительного механизма или машины.

Планетарный редуктор и планетарная передача — теория

Рассмотрен принцип действия планетарной передачи, указаны преимущества и недостатки применения планетарных редукторов. Приведена схема планетарной передачи и расчет передаточного отношения редуктора.

Планетарный редуктор и планетарная передача

Зубчатая передача

Зубчатая передача

Устройство планетарного механизма основано на вращении тел зубчатой передачи, которые непосредственно взаимодействуют с главным двигателем. Именно такое соединение и служит для передачи силы от редуктора до других механизмов с изменением скорости их вращения. Таким образом происходит передача крутящего момента от двигателя на колеса через основную ось, главную шестерню и сателлиты.
Вообще устройство зубчатой передачи достаточно простое и понятное. Вот, что входит в конструкцию обычной передачи.
Для соединения с главной передачей имеются две зубчатые шестерни, таким образом происходит зацепление. При движении происходит передача скорости вращения с главной шестерни на ведомую за счет зацепов. Наименьшее колесо в конструкции называется шестерней, а наибольшее будет главным и ведомым колесом.

Планетарный механизм

Схема планетарной передачи

Редукторы с зубчатой передачей, колеса которых имеют движущиеся оси, называются планетарными. Внутри расположены зубчатые колеса, перемещающиеся на своих, геометрических осях. Такие шестерни получили название сателлиты, потому что вся конструкция очень похожа на солнечную систему. Главные шестерни называются центральными колесами. Сателлиты крепятся на своих осях и вращаются вокруг главной передачи при помощи водила, которое движется так же, как и центральное колесо, вокруг главной оси. Центральное колесо остается неподвижным, а другие шестерни можно заблокировать или разблокировать полностью.

Если центральное колесо неподвижно, то второе постоянно движется. Ведущим здесь является вал подвижного колеса, а ведомым-водила. Если разблокировать все зубчатые колеса вместе с ведомым, то такая передача будет дифференциальной. Выделяют два основных и ведущих звена и одно ведомое.

При подробном рассмотрении простейшей планетарной передачи мы видим: ведущее колесо или водило, ведомое с тремя сателлитами, вращающимися вокруг центральной оси и центральное, неподвижное колесо.

Передаточное отношение

Чтобы рассчитать передаточное отношение редуктора, необходимо заметить определенное количество неподвижных звеньев(1,2,3 и Н) и условно задать им поступательное вращение со скоростью wH, равное скорости вращения водила, но с обратным знаком. Скорость зацепления зубчатых колес не изменяется. Таким образом скорость + wH +(- wH)=0, то есть водило будет остановлено. Если водило неподвижно, тогда планетарная передача превращается в зубчатую, где все колеса неподвижны. Сателлиты не учитываются. Их вращение будет положительным при одинаковом вращении шестерен, а отрицательным при противоположном вращении:i=(? 1 -? H)/(? 3 -? H)=-(z 3 /z 1), где z 1 и z. Если колесо 3 закреплено неподвижно, то угловая скорость водила Н = 1 /[1+(z 3 /z 1)], а передаточное отношение i =1+z 3 /z 1.

Как обычно, для работы редуктора с одноступенчатой передачей при больших нагрузках становится мало, поэтому стали изготавливать двух и трех ступенчатые редукторы, а иногда и четырех ступенчатые. Чаще всего применяется двухступенчатая передача.

Двухступенчатая планетарная передача.

Схема двухступенчатой планетарной передачи

Для других редукторов передаточное отношение высчитывается таким же способом. Для двухступенчатого редуктора, где центральное колесо 1—ведущее, водило Н2 — ведомое, центральные колеса 3 и 4 закреплены в корпусе, передаточное отношение i=1+z 2 z 3 /z 1 z 4.

При всех достоинствах планетарного редуктора, нужно знать, что при сильном вращении шестерни, КПД всего механизма сильно ухудшается.

Нагрузка от центрального колёса водила восприниматься всеми шестеренками (1-6) одинаково, при этом их размеры значительно меньше, чем у обычной передачи. Следовательно, главными преимуществами планетарной передачи являются большая скорость вращения, небольшой вес и компактность. Дифференциальные передачи используются в автомобиле для разложения движения, а так же в различных станках. К минусам такой передачи относится ее трудоемкое изготовление и сложная сборка на предприятии. Такие редукторы благодаря своим преимуществам находят свое применение во многих отраслях производства: в машиностроении, приборах, станкостроении, в транспорте.

Использован материал из книги «Детали машин» Гузенков П.Г.

Так же по теме предлагаем статью «Планетарный редуктор» с примером расчета передаточного отношения и анимированными схемами ступеней планетарного редуктора.

Определение понятия

Что же такое передаточное число редуктора? Любой редуктор служит для передачи крутящего момента с коробки передач на колеса. При этом скорость вращения всегда понижается. Передаточное число как раз и является показателем, во сколько раз это уменьшение происходит. К примеру, число 5,125, встречающееся в газелевских редукторах, показывает, что скорость вращения с входного вала на колеса уменьшается в 5,125 раза.

Практически редуктор в автомобиле располагается на ведущей оси. Если речь идёт о полноприводных вариантах – там имеется два редуктора, по одному на каждую ось. Отечественные автомобили производства ВАЗ и ГАЗ имеют задний редуктор, за некоторым исключением. Чтобы определить передаточное число редуктора, можно поступить несколькими способами:

• теоретический;
• практический;
• расчётный.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

u₁₂ = ± Z₂/Z₁ и u₂₁ = ± Z₁/Z₂,

Где u₁₂ – передаточное число шестерни и колеса;

Z₂ и Z₁ – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».

При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.

Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.

Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:

u₁₆ = u₁₂×u₂₃×u₄₅×u₅₆ = z₂/z₁×z₃/z₂×z₅/z₄×z₆/z₅ = z₃/z₁×z₆/z₄

Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.

КПД зубчатой передачи

Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:

• трение соприкасаемых поверхностей;
• изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
• потери на шпонках и шлицах;
• трение в подшипниках.

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.

Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.

При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы  узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.

Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.

Крутящий момент редуктора

Крутящий момент на выходном валу – вращающий момент на выходном валу. Учитывается номинальная мощность , коэффициент безопасности , расчетная продолжительность эксплуатации (10 тысяч часов), КПД редуктора.

Номинальный крутящий момент – максимальный крутящий момент, обеспечивающий безопасную передачу. Его значение рассчитывается с учетом коэффициента безопасности – 1 и продолжительность эксплуатации – 10 тысяч часов.

Максимальный вращающий момент – предельный крутящий момент, выдерживаемый редуктором при постоянной или изменяющейся нагрузках, эксплуатации с частыми пусками/остановками. Данное значение можно трактовать как моментальную пиковую нагрузку в режиме работы оборудования.

Необходимый крутящий момент – крутящий момент, удовлетворяющим критериям заказчика. Его значение меньшее или равное номинальному крутящему моменту.

Расчетный крутящий момент – значение, необходимое для выбора редуктора. Расчетное значение вычисляется по следующей формуле:

Mc2 = Mr2 x Sf ≤ Mn2

где Mr2 – необходимый крутящий момент; Sf – сервис-фактор (эксплуатационный коэффициент); Mn2 – номинальный крутящий момент.

Заключение

Рассмотрев различные примеры передаточных чисел редукторов автомобилей как отечественного, так и зарубежного производства, можно сделать несколько выводов. В первую очередь стало понятно, что передаточное число – важный параметр, характеризующий динамические и мощностные характеристики автомобиля. Зная только эту величину, можно понять, что собой представляет автомобиль в целом. Кроме этого, видно, насколько разнообразны редукторы даже на отечественных автомобилях.

В редуктор переднего/заднего моста автомобилей семейства НИВА можно установить любую главную передачу (пару) не зависимо от модели автомобиля. Чем больше передаточное число главной пары, тем, соответственно , больше мощность редуктора. Напротив, чем меньше передаточное число главной пары, тем редуктор является наиболее скоростным. Самыми лучшими мощностными характеристиками обладает редуктор ВАЗ 2102. В отношении полноприводных моделей ВАЗов справедливо правило: при ремонте редуктора (переднего или заднего в отдельности), необходимо обеспечить совпадение передаточных чисел у главных передач обоих редукторов. Несоблюдение данного правила неминуемо приведет к поломке зубьев шестерен главной передачи у одного или обоих редукторов сразу же после начала движения.

Главная пара	Передаточное число	кол-во зубьев на шестернях	число оборотов карданного вала на 10 оборотов колеса
на ведомой	на ведущей
2101	4,3	43	10	21,5
2102	4,44	40	9	22,2
2103	4,1	41	10	20,5
2106	3,9	43	11	19,5

Если Вы не знаете, какая именно главная пара и с каким передаточным числом установлена в редукторе Вашего автомобиля, можно воспользоваться получением необходимых данных следующим способом (нижеописанную операцию лучше производить с помощником):

Вывешивается одно заднее колесо автомобиля и устанавливаем его (автомобиль) на надежные подставки. Устанавливаем рычаг переключения передач в нейтральное положение так же как ираздатку и полностью отпускаем ручной тормоз, обеспечив, тем самым, свободное вращение колеса.

Вращаем поднятое колесо, считая при этом его обороты и обороты карданного вала. Для получения наиболее точных данных необходимо сделать 10 оборотов колеса. Подсчитав обороты колеса и карданного вала, используя приведенную выше таблицу, определяем передаточное число редуктора и, соответственно, модель главной пары. Если при ремонте в редуктор будет установлена не родная главная пара, с иным передаточным числом, то при движении изменятся показания спидометра (скорость и пройденный автомобилем путь).