Крутящий момент двигателя- что это и от чего зависит

Работа и мощность

Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила — любая сила — вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.

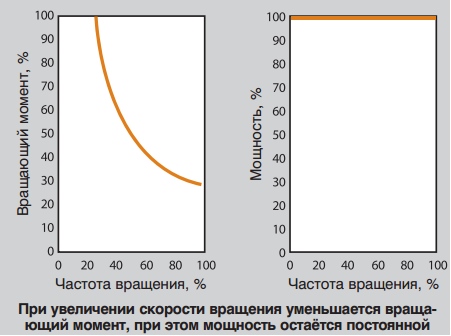
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).

Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.

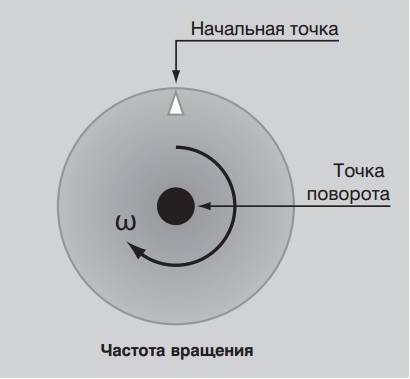
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.

Приведем единицы измерения к общему виду.

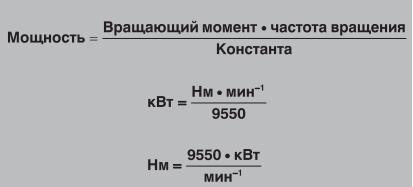
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.

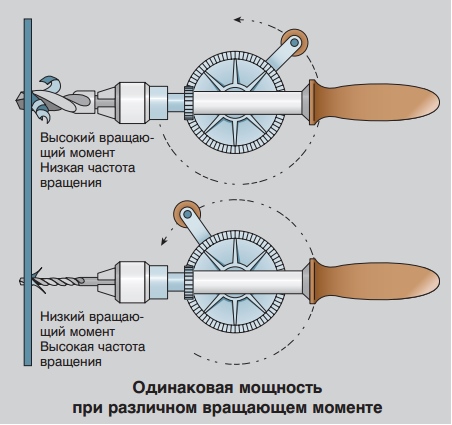
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.

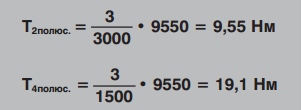
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.

Как образуется вращающий момент и частота вращения?

Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.

В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.

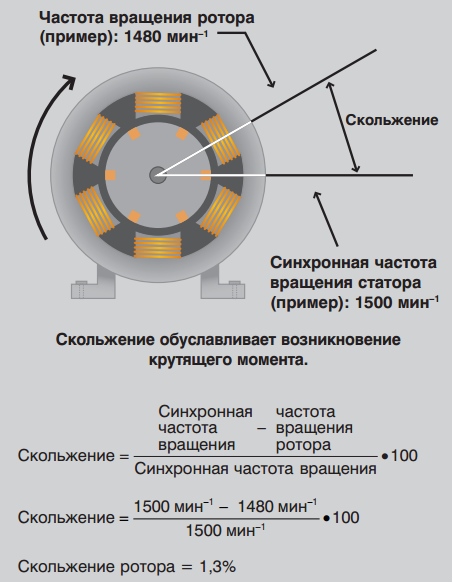
Скольжение
является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.

Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:

Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.

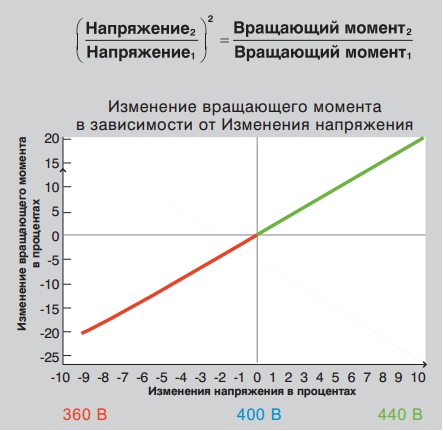
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.

В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).

Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 0,746) = 14,92 кВт.

И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.

Крутящий момент и лошадиная сила

Автолюбители нередко дискутируют друг с другом: чей двигатель мощнее. Но иногда и не представляют при этом, из чего складывается данный параметр. Общепринятый термин «лошадиная сила» был введён изобретателем Джеймсом Уаттом в XVIII веке.  Он придумал его, наблюдая за лошадью, которая была запряжена в поднимающий уголь из шахты механизм. Он рассчитал, что одна лошадь за минуту может поднять 150 кг угля на высоту 30-ти метров. Одна лошадиная сила эквивалентна 735,5 Ватт, или 1 кВт равен 1,36 л.с.

В первую очередь, мощность любого мотора оценивают в лошадиных силах, и лишь потом вспоминают о крутящем моменте. Но эта тяговая характеристика тоже даёт представление о конкретных тягово-динамических возможностях автомобиля. Крутящий момент является показателем работы силового агрегата, а мощность – основным параметром выполнения этой работы. Эти показатели тесно связаны друг с другом. Чем больше производится двигателем лошадиных сил, тем больше и потенциал крутящего момента. Реализуется этот потенциал в реальных условиях через трансмиссию и полуоси машины. Соединение этих элементов вместе и определяет, как именно мощность может переходить в крутящий момент.

Простейший пример – сравнение трактора с гоночной машиной. У гоночного болида лошадиных сил много, но крутящий момент требуется для увеличения скорости через редуктор. Чтобы такая машина двигалась вперёд, надо совсем немного работы, потому что основная часть мощности используется для развития скорости.

Что касается трактора, то у него может быть мотор с таким же рабочим объёмом, который вырабатывает столько же лошадиных сил. Но мощность в этом случае используется не для развития скорости, а для выработки тяги (См. тяговый класс). Для этого она пропускается через многоступенчатую трансмиссию. Поэтому трактор не развивает высоких скоростей, зато он может буксировать большие грузы, пахать и культивировать землю, и т.д.

В двигателях внутреннего сгорания сила передаётся от газов сгорающего топлива поршню, от поршня – передаётся на кривошипный механизм, и далее на коленчатый вал. А коленвал, через трансмиссию и приводы, раскручивает колёса.

Естественно, крутящий момент двигателя не постоянен. Он сильней, когда на плечо действует бо́льшая сила, и слабей – когда сила слабнет или перестаёт действовать. То есть, когда водитель давит на педаль газа, то сила, воздействующая на плечо, повышается, и, соответственно увеличивается крутящий момент двигателя.

Мощность обеспечивает преодоление всевозможных сил, которые мешают двигаться автомобилю. Это и сила трения в двигателе, трансмиссии и в приводах автомобиля, и аэродинамические силы, и силы качения колёс и т.д. Чем больше мощность, тем большее сопротивление сил машина сможет преодолеть и развить большую скорость. Однако мощность – сила не постоянная, а зависящая от оборотов мотора. На холостом ходу мощность одна, а на максимальных оборотах – совершенно другая. Многими автопроизводителями указывается, при каких оборотах достигается максимально возможная мощность автомобиля.

Необходимо учитывать, что максимальная мощность не развивается сразу. Автомобиль стартует с места практически при минимальных оборотах (немного выше холостого хода), и для того, чтобы отмобилизировать полную мощность, требуется время. Тут и вступает в дело крутящий момент двигателя. Именно от него и будет зависеть, за какой отрезок времени автомашина достигнет своей максимальной мощности – то есть, динамика её разгона.

Зачастую водитель сталкивается с такими ситуациями, когда требуется придать автомобилю значительное ускорение для выполнения необходимого маневра. Прижимая педаль акселератора в пол, он чувствует, что автомобиль ускоряется слабо. Для быстрого ускорения нужен мощный крутящий момент. Именно он и характеризует приёмистость автомобиля.

Основную силу в двигателе внутреннего сгорания вырабатывает камера сгорания, в которой воспламеняется топливно-воздушная смесь. Она приводит в действие кривошипно-шатунный механизм, а через него – коленчатый вал. Рычагом является длина кривошипа, то есть, если длина будет больше, то и крутящий момент тоже увеличится.

Однако увеличивать кривошипный рычаг до бесконечности невозможно. Ведь тогда придётся увеличивать рабочий ход поршня, а вместе с ним и размеры двигателя. При этом уменьшатся и обороты двигателя. Двигатели с большим рычагом кривошипного механизма можно применить только лишь в крупномерных плавательных средствах. А в легковых автомашинах с небольшими размерами коленчатого вала не поэкспериментируешь.

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы M = Fl M — момент силы F — сила l — плечо

Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.

Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.

На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.

То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.

Нагрузка насосов и типы нагрузки электродвигателя

Выделяют следующие типы нагрузок:

Постоянная мощность

Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.

Постоянный вращающий момент

Как видно из названия — «постоянный вращающий момент» — подразумевается, что величина вращающего момента, необходимого для приведения в действие какого- либо механизма, постоянна, независимо от скорости вращения. Примером такого режима работы могут служить конвейеры.

Переменный вращающий момент и мощность

«Переменный вращающий момент» — эта категория представляет для нас наибольший интерес. Этот момент имеет отношение к нагрузкам, для которых требуется низкий вращающий момент при низкой частоте вращения, а при увеличении скорости вращения требуется более высокий вращающий момент. Типичным примером являются центробежные насосы.

Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.

Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.

Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.

Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.

В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.

Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.

Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.

На рисунке показан центробежный насос в разрезе. Требования к вращающему моменту для такого типа нагрузки почти противоположны требованиям при «постоянной мощности». Для нагрузок при переменном вращающем моменте потребный вращающий момент при низкой частоте вращения — мал, а потребный вращающий момент при высокой частоте вращения — велик. В математическом выражении вращающий момент пропорционален квадрату скорости вращения, а мощность — кубу скорости вращения.

Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:

Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.

В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.

Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.

Величина I в физике

В последнем выражении предыдущего пункта величина I равна произведению массы точки на квадрат ее расстояния до оси, то есть:

Поскольку все реальные тела не являются материальными точками, а имеют определенные пространственные параметры и форму, то для определения их момента инерции используется исходное выражение выше, которое становится подынтегральным. Общая формула для I тела выглядит так:

Эта математическая формула говорит о том, что чтобы посчитать момент инерции всего тела его нужно мысленно разбить на материальные точки dm, умножить их на квадрат дистанции до оси вращения, а затем все результаты сложить.

Определение моментов инерции и маховых моментов частей приводов и систем

Формулы для определения моментов инерции и маховых моментов

1.Связь между моментом инерции и маховым моментом:

2.Моменты инерции тела, определяемый по кривой самоторможения в пределах угловых скоростей ω при израсходовании энергии W kW·sec на самоторможение:

3.Момент инерции тела, определяемый по раскачиванию (R’ – средний радиус подвязанного груза, T – время одного колебания, R — радиус тела):

4.Момент инерции, определяемый по падению груза G, подвешенного к шкиву радиуса R:

5.Момент инерции J тела, вращающегося с числом оборотов в минуту n1 и приведенного к валу, вращающемуся с числом n2 об/мин:

6.Пересчет поступательного движения массы m со скоростью v на вращательное движение с угловой скоростью ω:

7.Пересчет вращательного движения тела с моментом инерции J и угловой скоростью ω на поступательное движение со скоростью v:

8.Живая сила тела с маховым моментом GD, вращающегося с числом оборотов в минуту, равным n:

9.Маховой момент маховика, необходимый для совершения работы A kW·sec при изменении числа оборотов в минуту от n1 до n2:

10.То же, что и в предыдущем пункте, если известно среднее число оборотов в минуту nср и коэффициент неравномерности i:

11.Вес маховика, необходимый для совершения работы А при заданном коэффициенте неравномерности i и средней окружной скорости vср:

Источник

Единицы измерения момента силы

Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же — это вектор.

Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:

Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).

Число пусков электродвигателя в час

Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.

Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.

Предыстория

Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.

Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.

Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.

Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.

Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=α−π2{\displaystyle \beta =\alpha -{\frac {\pi }{2}}}, а так как cos⁡(α−π2)=sin⁡α{\displaystyle \cos {\left(\alpha -{\frac {\pi }{2}}\right)}=\sin \alpha }, получаем, что |F→|cos⁡β=|F→|sin⁡α{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.

Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sin⁡α{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin⁡(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.

Теперь видно, что произведение |r→||F→|sin⁡α{\displaystyle \left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin \alpha } есть не что иное, как модуль векторного произведения векторов r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}, то есть |r→×F→|{\displaystyle \left|{\vec {r}}\times {\vec {F}}\right|}, которое и было принято обозначить за момент силы M{\displaystyle M}, или модуль вектора момента силы |M→|{\displaystyle \left|{\vec {M}}\right|}.

Теперь полная работа записывается просто: A=∫φ|r→×F→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {r}}\times {\vec {F}}\right|d\varphi }, или A=∫φ|M→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {M}}\right|d\varphi }.

Крутящий момент в легковом и коммерческом транспорте

Интересно знать, что «кривые» ВСХ дизельных двигателей легковых авто
отличаются от грузовиков.

Разница дизельного ДВС легковушки и грузовика
Разница
дизельного ДВС легковушки и грузовика

Как можно увидеть, у
грузового ДВС нет выраженной «полки» момента. Это сделано неспроста. Для таких
авто важен пик тягового усилия, когда ему нужно тронуться с места и набрать
скорость. Дальше этот показатель не так важен – в ход идут лошадиные силы.
Разогнавшись, грузовик лишь поддерживает заданную скорость. «Размазав» полку тягового
усилия как у легкового ДВС, не получится нормально тронуться с места груженым.

Примеры решения задач

Пример

Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.

Решение. За основу решения задачи примем формулу, определяющую момент силы:

$$\bar{M}=\bar{r} \times \bar{F}(1.1)$$

В векторном произведении (видно из рисунка) $\bar{r} \neq 0, \bar{F} \neq 0$ . Угол между вектором силы и радиус –
вектором также будет отличен от нуля (или $180^{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.

Ответ. $\bar{M} \neq 0$

Слишком сложно?

Формула момента силы не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2.
В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?

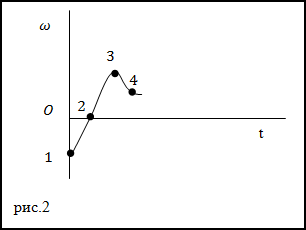
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:

$$M=I \varepsilon(2.1)$$

где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:

$$\varepsilon=\frac{d \omega}{d t}(2.2)$$

Перепишем (2.1), используя (2.2), имеем:

$$M=I \frac{d \omega}{d t}(2.3)$$

Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.

Ответ. M=0 в точке 3.

Читать дальше: Формула мощности.

Динамика вращения

В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:

Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.

Направление момента силы и его знак

Момент силы рассчитывают относительно точки, где он представляет собой вектор, или относительно оси, где есть лишь проекция вектора на ось.

Итак, берем точку Q — полюс, относительно которой рассчитывается момент силы. Далее следует провести радиус-вектор r из Q к F — точке приложения. Далее категория рассчитывается так:

\(M=\lbrack rF\rbrack\)

В результате получается вектор, длина которого определяется модулем:

\(\vert M\vert=\vert r\vert\ast\vert F\vert\ast\sin\varphi\)

Здесь φ является углом между векторами r и F.

Вектор М направлен так, что векторы r, F, M — правые. Это можно определить следующим образом. Ваше территориальное нахождение — на конце 3-го вектора, а на другие два направлен взгляд. Если самый короткий переход от вектора 1 к вектору 2 происходит против часовой стрелки, то они являются тройкой правых векторов. Если наоборот, т.е. по часовой стрелке, то они считаются левыми.

Затем следует совместить начала r и F путем параллельного переноса вектора F в Q. Через точку Q нужно провести ось перпендикулярно r и F. Возможны 2 направления — вниз или вверх.

Далее изобразите стрелку вектора на оси вверх. Оттуда посмотрите на направления r и F. Переход от одного вектора к другому также обозначьте стрелкой. Если стрелка указывает направление против часовой стрелки, то тройка векторов — правая. Это означает, что выбранное направление верно. В противном случае его необходимо сменить на противоположное.

Примечание

Правило правой руки определяет направление момента силы. Указательный палец совмещается с радиус-вектором, а средний — с вектором силы

От конца большого пальца, направленного вверх, обратите внимание на оба вектора: при переходе от указательного к среднему происходит против часовой стрелки направление момента силы аналогично направлению, показанному большим пальцем; переход против часовой говорит о противоположном направлении

Что касается знака, то момент силы относительно любой точки имеет знак:

• по направлению часовой стрелки — минус (-);
• против направления часовой стрелки — плюс (+).

Как увеличить крутящий момент

Увеличение рабочего объема. Чтобы повышать КМ используются разные методы: замена установленного коленвала на вал с увеличенным эксцентриситетом (редко встречающаяся запчасть, которую трудно находить) или расточка цилиндров под больший диаметр поршней. Оба способа имеют свои плюсы и минусы. Первый требует много времени на подбор деталей и снижает долговечность двигателя. Второй, увеличение диаметра цилиндров с помощью расточки, более популярен. Это может сделать практически любой автосервис. Там же можно настроить карбюратор для повышения КМ.

Изменение величины наддува. Турбированные двигатели позволяют достичь более высокого показателя КМ благодаря особенностям конструкции – возможности отключить ограничения в блоке управления компрессором, который отвечает за наддув. Манипуляции с блоком позволят повысить объем давления выше максимума, указанного производителем при сборке автомобиля. Способ можно назвать опасным, поскольку у каждого двигателя есть лимитированный запас нагрузок. Кроме того, часто требуются дополнительные усовершенствования: увеличение камеры сгорания, приведение охлаждения в соответствие повышенной мощности. Иногда требуется отрегулировать впускной клапан, иногда – сменить распредвал. Может потребоваться замена чугунного коленвала на стальной, замена поршней.

Изменение газодинамики. Редко используемый вариант, поскольку двигатель – сложная конструкция, созданием которого занимаются профессионалы. Теоретически можно придумать, как убрать ограничения, заложенные конструкторами для увеличения срока эксплуатации двигателя и его деталей. Но на практике, если убрать ограничитель, результат не гарантирован, поскольку поменяются все характеристики: например, динамика вырастет, но шина не будет цепляться за дорогу. Чтобы усовершенствовать двигатель такие образом надо быть не просто автомобильным конструктором, но и математиком, физиком и т.д.

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.

Заключение

В это статье мы рассмотрели, чем отличаются термины «момент силы» и «вращающий момент», а также английские термины «moment of force» и «torque», и увидели несколько примеров момента силы. В основном мы говорили о случаях, когда момент силы создает проблемы в строительстве, но часто бывает наоборот и момент силы приносит пользу. Примеры использования момента силы на практике — в статье «Подробнее о вращающем моменте». Стоит также упомянуть, что разница в терминологии в английском языке чаще всего значительна в американском и британском машиностроении и строительстве, в то время как в физике эти термины часто взаимозаменяемы.

Автор статьи: Kateryna Yuri